基础算法—回溯篇

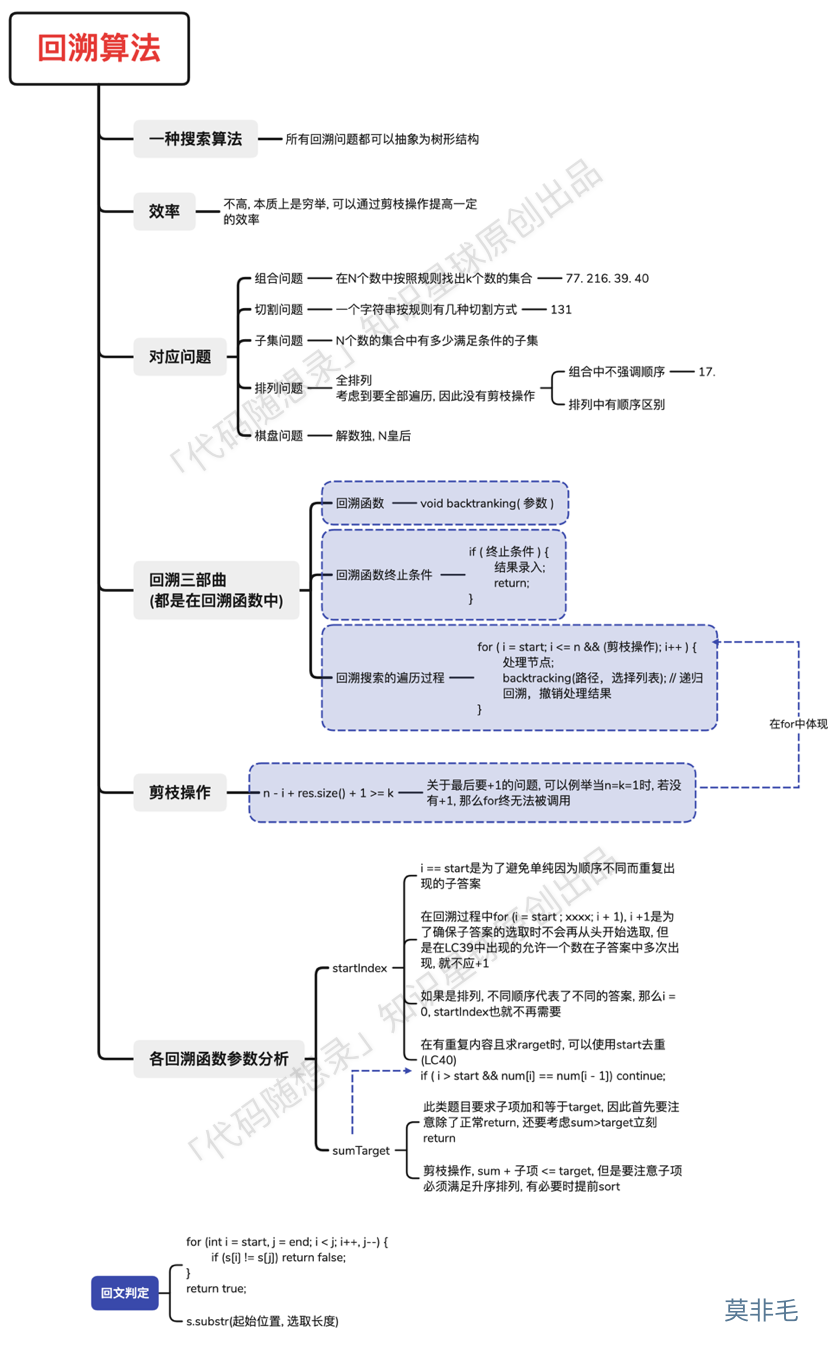
什么是回溯法

回溯法也可以叫做回溯搜索法，它是一种搜索的方式。

回溯是递归的副产品，只要有递归就会有回溯。

回溯法的效率

回溯的本质是穷举，穷举所有可能，然后选出我们想要的答案，如果想让回溯法高效一些，可以加一些剪枝的操作，但也改不了回溯法就是穷举的本质。

回溯法解决的问题

一般可以解决如下几种问题：

组合问题：N个数里面按一定规则找出k个数的集合
切割问题：一个字符串按一定规则有几种切割方式
子集问题：一个N个数的集合里有多少符合条件的子集
排列问题：N个数按一定规则全排列，有几种排列方式
棋盘问题：N皇后，解数独等等

组合是不强调元素顺序的，排列是强调元素顺序。

例如：{1, 2} 和 {2, 1} 在组合上，就是一个集合，因为不强调顺序，而要是排列的话，{1, 2} 和 {2, 1} 就是两个集合了。

记住组合无序，排列有序，就可以了。

回溯法模板

回溯法解决的问题都可以抽象为树形结构，是的，我指的是所有回溯法的问题都可以抽象为树形结构！

因为回溯法解决的都是在集合中递归查找子集，集合的大小就构成了树的宽度，递归的深度，都构成的树的深度。

递归就要有终止条件，所以必然是一棵高度有限的树（N叉树）。

回溯三部曲

回溯函数模板返回值以及参数
- 回溯函数伪代码如下：

1 2	`//回溯算法中函数返回值一般为void void backtracking(参数)`

回溯函数终止条件
- 什么时候达到了终止条件，树中就可以看出，一般来说搜到叶子节点了，也就找到了满足条件的一条答案，把这个答案存放起来，并结束本层递归。

if (终止条件) {
    存放结果;
    return;
}

回溯搜索的遍历过程

for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
    处理节点;
    backtracking(路径，选择列表); // 递归
    回溯，撤销处理结果
}

for循环就是遍历集合区间，可以理解一个节点有多少个孩子，这个for循环就执行多少次。

backtracking这里自己调用自己，实现递归。

大家可以从图中看出for循环可以理解是横向遍历，backtracking（递归）就是纵向遍历，这样就把这棵树全遍历完了，一般来说，搜索叶子节点就是找的其中一个结果了。

回溯算法模板框架如下：

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

解题模板

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    LinkedList<Integer> list = new LinkedList<>();
    public List<List<Integer>> main() {
        backtracking(index);
        return res;
    }
    public void backtracking(int index){
        if(list.size()==目标大小){
            res.add(new ArrayList(list));
            return;
        }
        剪枝语句
        for(int i=index;i<=n;i++){
            list.add(i);
            		//i+1不可以重复使用，i可以重复使用
            backtracking(i+1);
            list.removeLast();
        }
    }
}