前缀和
前缀和主要适用的场景是原始数组不会被修改的情况下,频繁查询某个区间的累加和。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| class PrefixSum {
private int[] prefix;
public PrefixSum(int[] nums) {
prefix = new int[nums.length + 1];
for (int i = 1; i < prefix.length; i++) {
prefix[i] = prefix[i - 1] + nums[i - 1];
}
}
public int query(int i, int j) {
return prefix[j + 1] - prefix[i];
}
}
|
一维前缀和
思路
除自身以外数组的乘积(上三角,下三角)
同余定理
1
2
3
| 前缀数组sum,sum[i]表示前i个元素的和。
子数组nums[i..j]的和 subNum = sum[j+1]-sum[i];
※同余定理: subNum % k == 0,等价于 sum[j+1] % k == sum[i] % k !!!(j>i)
|
思路
前缀和 + 哈希表
将问题转化为:如何求得最长一段区间和为 0 的子数组。 同时使用「哈希表」来记录「某个前缀和出现的最小下标」是多少。
思路
使数组元素全部相等的最少操作次数
前缀和+二分
1.先将数组进行排序,接着二分查找与queries[i]最接近的数的下标,因此:nums[i]前的数一定小于queries[i],nums[i]后的数一定大于queries[i]。
2.在 nums 中小于 queries[i] 的部分计算方式为:这部分数字个数 * queries[i] - 这部分数字总和;
大于 x 部分的计算方式为:这部分数字总和 - queries[i] * 这部分数字个数
步骤2可以利用前缀和加速
思路
和2602类似
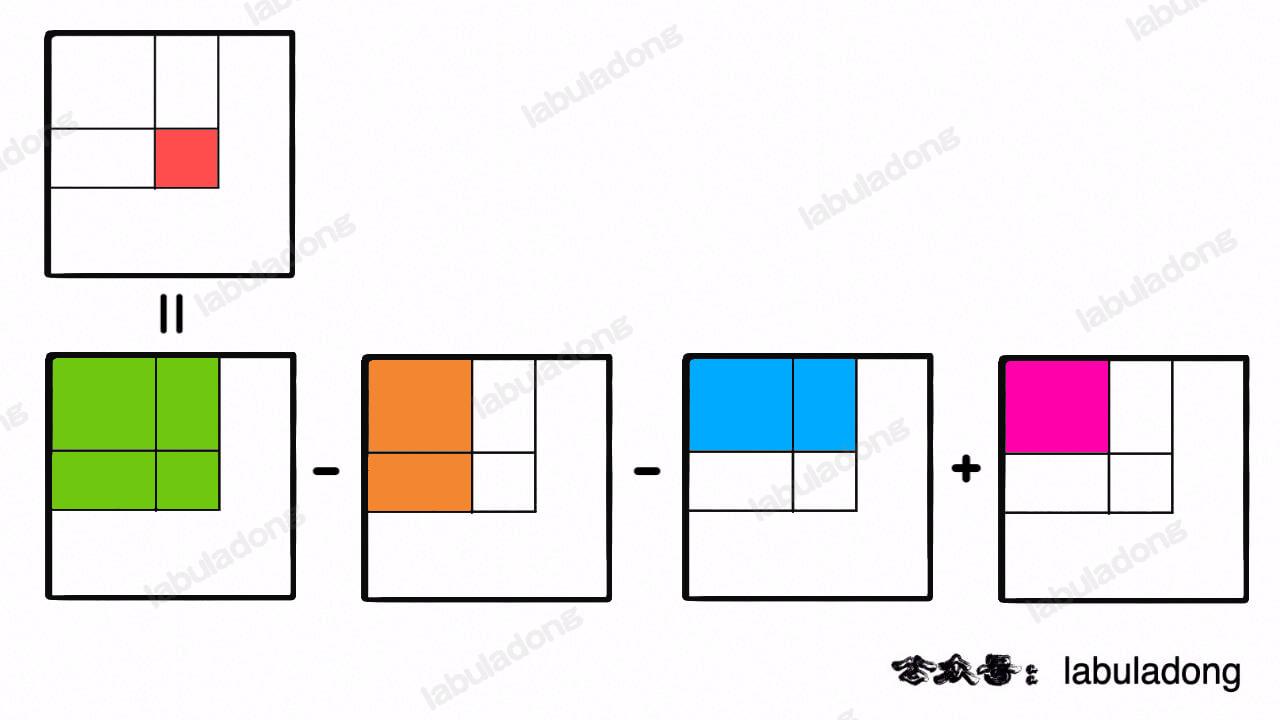
二维前缀和
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| class NumMatrix {
private int[][] preSum;
public NumMatrix(int[][] matrix) {
int m = matrix.length, n = matrix[0].length;
if (m == 0 || n == 0) return;
preSum = new int[m + 1][n + 1];
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
preSum[i][j] = preSum[i-1][j] + preSum[i][j-1] + matrix[i - 1][j - 1] - preSum[i-1][j-1];
}
}
}
public int sumRegion(int x1, int y1, int x2, int y2) {
return preSum[x2+1][y2+1] - preSum[x1][y2+1] - preSum[x2+1][y1] + preSum[x1][y1];
}
}
|
差分
差分数组的主要适用场景是频繁对原始数组的某个区间的元素进行增减。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
class Difference {
private int[] diff;
public Difference(int[] nums) {
diff = new int[nums.length];
diff[0] = nums[0];
for (int i = 1; i < nums.length; i++) {
diff[i] = nums[i] - nums[i - 1];
}
}
public void increment(int i, int j, int val) {
diff[i] += val;
if (j + 1 < diff.length) {
diff[j + 1] -= val;
}
}
public int[] result() {
int[] res = new int[diff.length];
res[0] = diff[0];
for (int i = 1; i < diff.length; i++) {
res[i] = res[i - 1] + diff[i];
}
return res;
}
}
|
基于前缀和的差分数组
一维
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
| import java.io.*;
public class Main {
public static StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in), 32768));
public static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
public static int nextInt() throws IOException {in.nextToken();return (int) in.nval;}
public static void main(String[] args) throws Exception {
int n = nextInt();
int m = nextInt();
int[] nums = new int[n+1];
for (int i = 1; i <=n; i++) {
nums[i]=nextInt();
}
int[] diff = new int[n+1];
for (int i = 1; i <=n; i++) {
insert(diff,i,i,nums[i]);
}
for (int i = 0; i < m; i++) {
insert(diff,nextInt(),nextInt(),nextInt());
}
for (int i = 1; i <=n; i++) {
diff[i]+=diff[i-1];
out.print(diff[i]+" ");
}
out.close();
}
public static void insert(int[] diff,int l,int r,int val){
diff[l]+=val;
if (r+1<diff.length){
diff[r+1]-=val;
}
}
}
|
二维
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
| import java.io.*;
public class Main {
public static StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in), 32768));
public static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
public static int nextInt() throws IOException {in.nextToken();return (int) in.nval;}
public static void main(String[] args) throws Exception {
int n = nextInt();
int m = nextInt();
int q = nextInt();
int[][] nums = new int[n+2][m+2];
for (int i = 1; i <=n; i++) {
for (int j = 1; j <=m; j++) {
nums[i][j]=nextInt();
}
}
int[][] diff = new int[n+2][m+2];
for (int i = 1; i <=n; i++) {
for (int j = 1; j <=m; j++) {
insert(diff,i,j,i,j,nums[i][j]);
}
}
for (int i = 0; i < q; i++) {
insert(diff,nextInt(),nextInt(),nextInt(),nextInt(),nextInt());
}
for (int i = 1; i <=n; i++) {
for (int j = 1; j <=m; j++) {
diff[i][j]+=diff[i-1][j]+diff[i][j-1]-diff[i-1][j-1];
out.print(diff[i][j]+" ");
}
out.println();
}
out.close();
}
public static void insert(int[][] diff,int x1,int y1,int x2,int y2,int val){
diff[x1][y1]+=val;
diff[x2+1][y1]-=val;
diff[x1][y2+1]-=val;
diff[x2+1][y2+1]+=val;
}
}
|
